This is a follow-up of my previous post about the similarities between the patterns found on the complex division and some quasicrystal diffraction patterns.
"If the doors of perception were cleansed, everything would appear to man as it is: infinite". William Blake's "The Marriage of Heaven and Hell"
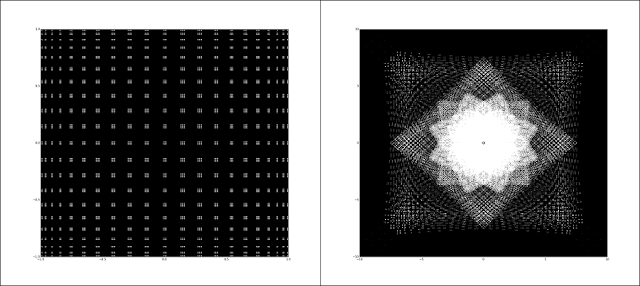
In the previous post, I showed the results of a complex division test where the original complex plane points are a lattice of points z=[-a,a]+[-a,a]i where a is an integer. Let us call L to the set of complex points z of this lattice. Those lattice points form a mesh of points in the complex plane. When the complex division is performed over the lattice (this means that every z complex number of L is divided by the rest of the points of L and itself) the result is a pattern that initially looks similar to some quasicrystal diffraction patterns (please see my previous post for videos and plottings). Below, left side, the original complex plane lattice points and in the right side the pattern that is generated applying complex division over the lattice points as explained above. These examples are made for a lattice L whose value a is 41, so z=[-41,41]+[-41,41]i. This means that the original lattice L is including 83x83 = 6889 complex numbers.
I wanted to know how the transformation of the original lattice modified the resulting pattern, so I have started to test the trigonometric functions applied to the original lattice points. The results are also quite amazing. Here is a briefing about it:
1. Transformation of the complex numbers z of L as follows: z=sin([-a,a])+sin([-a,a])i. Left side, the result of the transformation of L and in the right side the pattern that is generated.
Here is a video zooming in and out the pattern:
2. Transformation of the complex numbers z of L as follows: z=cos([-a,a])+cos([-a,a])i. Left side, the result of the transformation of L and in the right side the pattern that is generated.
It is a little bit similar to the sine transformation, but it is not identical. It is possible also to make hybrids of sine and cosine functions and the resulting patterns are variations of the patterns shown above.
Here is a video zooming in and out the pattern:
3. Transformation of the complex numbers z of L as follows:
z=cosec([-a,a])+cosec([-a,a])i. Left side, the result of the transformation
of L and in the right side the pattern that is generated.
Here is a video zooming in and out the pattern:
Here is a video zooming in and out the pattern:
5. Transformation of the complex numbers z of L as follows:
z=arctan([-a,a])+arctan([-a,a])i. Left side, the result of the transformation
of L and in the right side the pattern that is generated.
Here is a video zooming in and out the pattern:
Some of the trigonometric transformations look similar, but they are not exactly the same patterns. These are some zoomed plottings of them:
1. Sine pattern:
2. Cosine pattern:
3. Cosecant pattern:
4. Cotangent pattern:
5. Arctangent pattern:
Finally, here are some plottings of the closest points to 0+0i, from left to right, top-down, cosine, sine, cosecant, cotangent, tangent, secant. The cosine and sine, cosecant and secant and cotangent and tangent patterns look similar:
I am still testing some other transformations of the original lattice L, but initially they are not so interesting. I will post them in a former post. Some days ago Terence Tao posted an article named "Sweeping a matrix rotates its graph" explaining the technique named "Sweeping" performed over squared matrices which is also based on division by selecting a pivot point of the main diagonal of the matrix. I will try to use that technique setting up the lattice L as a matrix of complex numbers and see what happens, the results could be a variation of these ones. If somebody reading this knows more about these type of patterns please let me know to share ideas.