Galois theory and cyclic groups

Just an excerpt from Wikipedia... I am currently reading the book "Symmetry: A Mathematical Exploration" (Springer, Kristopher Tapp)". Is a good reading for beginners (like myself). Amazingly thanks to that great book I started to understand this kind of relationships:

"An $n^{th}$ root of unity may be thought of as a complex number whose $n^{th}$ power is $1$. That is, it is a root of the polynomial $x^n − 1$. The $n^{th}$ roots of unity form a cyclic group of order $n$ under multiplication. For example, the polynomial $0 = z^3 − 1$ factors as $(z − s^0)(z − s^1)(z − s^2)$, where $s = e^{2 \pi i / 3}$; the set $ \{ s^0, s^1, s^2 \} $ forms a cyclic group under multiplication. The Galois group of the field extension of the rational numbers generated by the $n^{th}$ roots of unity forms a different group. It is isomorphic to the multiplicative group modulo $n$, which has order $\phi(n)$ and is cyclic for some but not all $n$."

Converting complex domain coloring visualizations into autostereograms

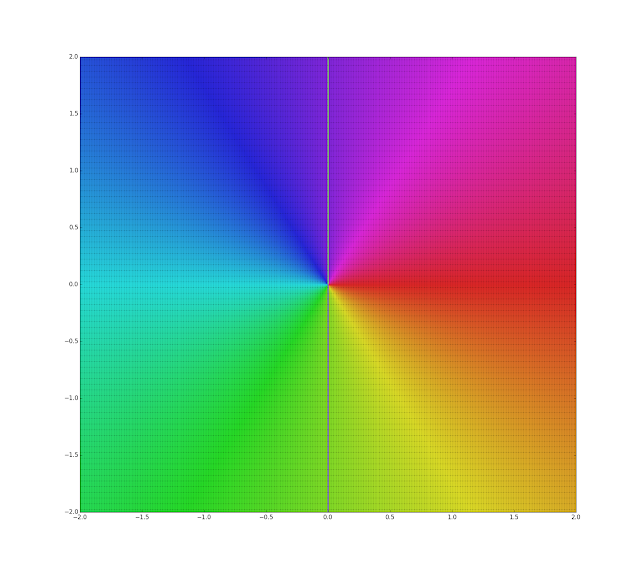
As Wikipedia says regarding the domain coloring technique for complex functions:

"A graph of a complex function $g : \Bbb C \to \Bbb C $ of one complex variable lives in a space with two complex dimensions. Since the complex plane itself is two-dimensional, a graph of a complex function is an object in four real dimensions. That makes complex functions difficult to visualize in a three-dimensional space. "

The domain coloring technique transforms the points belonging to $f(z)$ into hue, brightness and saturation values, all normalized into $[0,1]$. Usually the argument of the complex number $f(z)$ is converted into a normalized value $[0,1]$ and then associated to a hue value. Then the color associated to $f(z)$ is shown at the position $z$.

For instance, $f(z)=z^3+1$. This is how looks the interval $z=[+/-]4+[+/-]3i$:

So far so good. But we cannot perceive the sense of depth. So what I want to do is bringing up that depth using autostereograms.

My first idea was applying directly the normalized color map as depth map, and then create the autostereogram. The normalized color map shown above is converted into the following depth map:

And then it is possible to create the autostereogram. It is of the "wall-eyed" ("parallel") convergence type (non-cross eyed). The three-dimensional effect can be produced by both eyes looking at a the image by defocusing the eyes at a certain distance. The examples are fine-tuned to be seen at a distance around $30-40$cm (click in the image to see a full screen view):

There is a trick: it is included a subtle layer with the original color map, and then added transparency to the autostereogram (alpha=0.9). In that way, the original color map can be slightly seen and works as a color texture over the autostereogram, so when we look at it, we can see that colors and depth are matching.

Two more examples: $f(z)=z^5-1$ and $f(a+bi)=\tan{(ab)}+atan(ab)i$:

Indeed it is possible to make also animations once the eye gets used to the correct focal length. I wonder if this technique is in use (e.g. educational purposes). Initially it seems very interesting! I have added a question at MSE regarding this topic.

Complex Domain coloring vs Complex Range (over the output) coloring: which one brings more information?

Recently I have made a question regarding the Complex Domain coloring technique at MSE.

Basically, as Wikipedia says: 

"Domain coloring is a technique for visualizing functions of a complex variable ...There were many earlier uses of color to visualize complex functions, typically mapping argument (phase) to hue."

So basically I have learned how to do the basic hue map when we have a complex  injective function $f(z)$. These are some simple examples:

$(1)\ f(z)=\frac{1}{z}$ 

$(2)\ f(z)=\frac{(z^2-1)(z-2-i)^2}{z^2+2+2i}$

$(3)\ f(z)=z^3+1$ 

$(4)\ f(z)=z^5-1$.

$(5)\ f(z)=e^z$.

They are the mappings we are used to see. But to my surprise, then I tried a "reverse" mode, instead of mapping over the positions of the input complex points (the domain of the function), mapped the output points with the conversion to hue of the original input points, a kind of "Range coloring" or "Image coloring" or "coloring map over the result" of the function, the results were also very impressive. They are the other side of the coin of the relationship between the Domain and the Image/Range of the function (in the same order than before): 

As usual, this is the Python code I have prepared to create the graphics. Feel free to use it and modify it:

def hsl_rgb_visu():

    def hslToRgb(h, s, l):
        # Source: https://stackoverflow.com/questions/2353211/hsl-to-rgb-color-conversion
        # Converts an HSL color value to RGB. Conversion formula
         # adapted from http://en.wikipedia.org/wiki/HSL_color_space.
         # Assumes h, s, and l are contained in the set [0, 1] and
         # returns r, g, and b in the set [0, 255].
        def hue2rgb(p, q, t):
            if t < 0:
                t += 1
            if t > 1:
                t -= 1
            if t < 1/6:
                return p + (q - p) * 6 * t
            if t < 1/2:
                return q
            if t < 2/3:
                return p + (q - p) * (2/3 - t) * 6
            return p
      
        r,g,b = 0,0,0

        if s == 0:
            r,g,b = l,l,l
        else:
            q=0
            if l < 0.5:
                q=l * (1 + s)
            else:
                q=l + s - l * s
              
            p = 2 * l - q;
            r = hue2rgb(p, q, h + 1/3)
            g = hue2rgb(p, q, h)
            b = hue2rgb(p, q, h - 1/3)
      
        prevR=str(hex(round(r * 255))).replace("0x","")
        prevG=str(hex(round(g * 255))).replace("0x","")
        prevB=str(hex(round(b * 255))).replace("0x","")
      
        if len(prevR)==1:
            prevR="0"+prevR
        if len(prevG)==1:
            prevR="0"+prevR
        if len(prevB)==1:
            prevR="0"+prevR
          
        return "#"+prevR+prevG+prevB
      
    from sympy import mobius, factorint, totient
    from gmpy2 import is_prime, is_square
    import matplotlib.pyplot as plt
    import csv
    from random import randint
    from math import sqrt, log, cos , sin , tan, pi, atan2, acos, pi
    import numpy as np
    import cmath as cmath
    import fractions
   
    def lcm(a,b): return abs(a * b) / fractions.gcd(a,b) if a and b else 0
   
    testlimit = 200
    testbase = 100
   
    lx=[]
    ly=[]
    lc=[]
   
    lh=[]
    ll=[]
    lr=[]
    ls=[]
   
    print("Calculating...")
    maxx=0
    maxy=0
    for posx in range(-testlimit,testlimit+1):
        for posy in range(-testlimit,testlimit+1):
      
            x=posx/testbase
            y=posy/testbase
          
            # Make function
          
            # function indentity
            #resx = x
            #resy = y
            #maxx = testlimit**2
            #maxy = testlimit**2
          
            # function complex multiplicative inverse 1/z example0
            #myc=x+(y*(1j))
            #if myc == 0:
            #    myc = 0
            #else:
            #    myc=1/myc
          
          
            # function complex example1
            #myc=x+(y*(1j))
            #myc=(((myc**2)-1)*(myc-2-(1j))**2)/((myc**2)+2+(2j))
          
            # function complex example2
            #myc=x+(y*(1j))
            #myc=(myc**3)+1
          
            # function complex z^5-1 example3
            #myc=x+(y*(1j))
            #myc=(myc**5)-1
          
            # function complex exp, asin, atan, acos, sin, tan, cos (con h) example4
            myc=x+(y*(1j))
            myc=cmath.exp(myc)
          
            resx=myc.real
            resy=myc.imag
          
            # Make the inverse mapping
            #if abs(resx)>5 or abs(resy)>5:
            #    continue
          
            # Make the inverse mapping
            #tmpresx = resx
            #tmpresy = resy
            #resx=x
            #resy=y
          
          
            if abs(resx)>maxx:
                maxx=abs(resx)
            if abs(resy)>maxy:
                maxy=abs(resy)
          
            current_angle = 0
            current_r = sqrt((resx**2)+(resy**2))
            if resx!=0:
                current_angle = atan2(resy,resx)
            else:
                if y>0:
                    current_angle = pi/2
                else:
                    current_angle = (pi/2)*3
              
            if current_angle < 0:
                current_angle = current_angle + (2*pi)
          
            current_angle = (1/(2*pi))*current_angle
              
            h = current_angle
            l = 0.5
            s = 0.7
          
            lx.append(x)
            ly.append(y)
          
            # Make the inverse mapping
            #lx.append(tmpresx)
            #ly.append(tmpresy)
          
            lh.append(h)  
            ll.append(l)  
            ls.append(s)
            lr.append(current_r)  
          
    base=1/(sqrt((maxx**2)+(maxy**2)))
    for i in range(0,len(lx)):
        #ls[i] = 0.88-(base*lr[i])
        #ll[i] = 1-(1/(2**(1+(base*abs(lr[i])))))
        lc.append(hslToRgb(lh[i], ls[i], ll[i]))
          
    print("Plotting...")
    ax = plt.gca()
    ax.set_axis_bgcolor((0, 0, 0))
    figure = plt.gcf()
    figure.set_size_inches(18, 16)
    for i in range(0,len(lx)):
        print("Current index="+str(i)+" of "+str(len(lx)-1)+"\r", end='')
        plt.plot(lx[i],ly[i],".",color=lc[i])
    plt.savefig("visualize_4var_functions_with_colors.png")
    #plt.show()
    print("End...")
   
hsl_rgb_visu()

I think that in terms of Complex Domain coloring still there are things to explode and we are still seeing only one side of the coin. And the other side seems quite interesting!