About the similarities between the patterns found on the Complex Division and some Quasicrystal diffraction patterns (II): trigonometric transformations of the lattice points

This is a follow-up of my previous post about the similarities between the patterns found on the complex division and some quasicrystal diffraction patterns.

"If the doors of perception were cleansed, everything would appear to man as it is: infinite". William Blake's "The Marriage of Heaven and Hell"

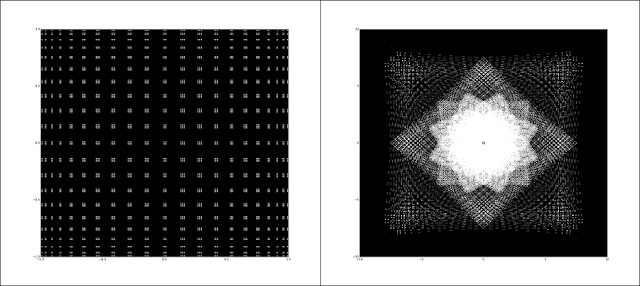
In the previous post, I showed the results of a complex division test where the original complex plane points are a lattice of points z=[-a,a]+[-a,a]i where a is an integer. Let us call L to the set of complex points z of this lattice. Those lattice points form a mesh of points in the complex plane. When the complex division is performed over the lattice (this means that every z complex number of L is divided by the rest of the points of L and itself) the result is a pattern that initially looks similar to some quasicrystal diffraction patterns (please see my previous post for videos and plottings). Below, left side, the original complex plane lattice points and in the right side the pattern that is generated applying complex division over the lattice points as explained above. These examples are made for a lattice L whose value a is 41, so z=[-41,41]+[-41,41]i. This means that the original lattice L is including 83x83 = 6889 complex numbers.

I wanted to know how the transformation of the original lattice modified the resulting pattern, so I have started to test the trigonometric functions applied to the original lattice points. The results are also quite amazing. Here is a briefing about it:

1. Transformation of the complex numbers z of L as follows: z=sin([-a,a])+sin([-a,a])i. Left side, the result of the transformation of L and in the right side the pattern that is generated.

Here is a video zooming in and out the pattern:

2. Transformation of the complex numbers z of L as follows: z=cos([-a,a])+cos([-a,a])i. Left side, the result of the transformation of L and in the right side the pattern that is generated.

It is a little bit similar to the sine transformation, but it is not identical. It is possible also to make hybrids of sine and cosine functions and the resulting patterns are variations of the patterns shown above.

Here is a video zooming in and out the pattern:

3. Transformation of the complex numbers z of L as follows: z=cosec([-a,a])+cosec([-a,a])i. Left side, the result of the transformation of L and in the right side the pattern that is generated.

Here is a video zooming in and out the pattern:

4. Transformation of the complex numbers z of L as follows: z=cotan([-a,a])+cotan([-a,a])i. Left side, the result of the transformation of L and in the right side the pattern that is generated. 

Here is a video zooming in and out the pattern:

5. Transformation of the complex numbers z of L as follows: z=arctan([-a,a])+arctan([-a,a])i. Left side, the result of the transformation of L and in the right side the pattern that is generated.

Here is a video zooming in and out the pattern:

Some of the trigonometric transformations look similar, but they are not exactly the same patterns. These are some zoomed plottings of them:

1. Sine pattern:

2. Cosine pattern:

 3. Cosecant pattern:

4. Cotangent pattern:

5. Arctangent pattern:

Finally, here are some plottings of the closest points to 0+0i, from left to right, top-down, cosine, sine, cosecant, cotangent, tangent, secant. The cosine and sine, cosecant and secant and cotangent and tangent patterns look similar:

I am still testing some other transformations of the original lattice L, but initially they are not so interesting. I will post them in a former post. Some days ago Terence Tao posted an article named "Sweeping a matrix rotates its graph" explaining the technique named "Sweeping" performed over squared matrices which is also based on division by selecting a pivot point of the main diagonal of the matrix. I will try to use that technique setting up the lattice L as a matrix of complex numbers and see what happens, the results could be a variation of these ones. If somebody reading this knows more about these type of patterns please let me know to share ideas.

About the similarities between the patterns found on the Complex Division and some Quasicrystal diffraction patterns

As the brilliant and wise professor William Thurston said: "Mathematics is an art of human understanding. … Our brains are complicated devices, with many specialized modules working behind the scenes to give us an integrated understanding of the world. Mathematical concepts are abstract, so it ends up that there are many different ways they can sit in our brains. A given mathematical concept might be primarily a symbolic equation, a picture, a rhythmic pattern, a short movie — or best of all, an integrated combination of several different representations."

In the case of the following test, the concepts are pictures and movies. As in my former post regarding the patterns that can be found in the roots of quadratic and cubic equations, I wanted to know if there are patterns hidden in the complex division, and it seems I found some interesting too!  

Indeed, reviewing the results of my former post, and thanks to the kind insights from the administrator of the Number Theory group in LinkedIn, it seems that they look like the patterns of the refraction of some type of quasicrystal structures. Are they related? I do not know, but so far here is what I have found:

1. First this is the description of the test:  the images are showing the set S of complex numbers a+bi represented in the Cartesian plane (a=x, b=y) obtained from the divisions of the complex numbers: z1/z2 , where z1 = (A+Ai) and z2 =  (B+Bi) being A and B natural numbers both of the interval [-41..41]. The set S contains all the possible combinations of divisions between z1 and z2 in those intervals (except when z2=0+0i which is not represented). Then a zoom is applied to show only a zoomed part of the whole pattern.

2. As the intervals used for the test are the same ones, A = B = [-41..41], this is the original lattice or mesh of complex numbers that will be divided between the whole same mesh of complex numbers (every point of this image represents a complex number and the output of the test is the division of each one of those complex numbers by all the complex numbers of the mesh)

3. This is a zoom-out to see the result of the complex division. This is the complete set S seen from the interval x=y=[-50,50]. As it can be seen in the image, due to the complex division formula, different meshes representing different subsets of the complex division are generated rotating on the center 0+0i. Up to the interval x=y=[-1..1], the closer we are to the center, the more different meshes are swapped, and the denser it is the quantity of complex numbers of the set. For smaller intervals inside x=y=[-1..1] (e.g. x=y=[-0.5,0.5]) the closer we get to the center (I will call it nucleus too) the darker it gets. The peak of density is at x=y=[-1..1], so the image is brighter when it is zoomed on that interval. Clicking in the image it is possible to see details on the structures that are generated due to the swapping of the meshes. They are similar to tessellations.

4. This is a zoom-in in the frame x,y in [-1.2,1.2]. There is symmetry in both axis, X and Y.

5. Zooming-in even more, it is possible to see how it looks like the nucleus near 0+0i, this is x,y in [-0.1,0.1]. The more meshes are swapped the more interesting patterns appear. The image below is obtained by using the intervals A=B=[-81..81] instead of A=B=[-41..41] because the closer we get into the center inside x=y=[-1..1] the darker it is, so it is required a bigger set S to have more density and bright (so the pattern closer to the nucleus is easier to see).

Summarizing, the following video shows a zoom-in, zoom-out into the patterns that can be seen in the set of complex numbers obtained from the divisions of the complex numbers: z1/z2 , where z1 = (A+Ai) and z2 =  (B+Bi) where A and B are natural numbers in the interval [-41..41]. The set generates all the possible combinations of divisions between z1 and z2 in those intervals.

So far those are the results of the test. Now, what similarities can be found between those images and the refraction patterns of quasicrystals? Let us compare. 

1. Something basic,  credits to the Wikipedia, this is the X-ray diffraction pattern of the natural Al₆₃Cu₂₄Fe₁₃ quasicrystal.

2. Credits to Steffen Weber, this is a simulation of diffraction pattern, which could represent either electron diffraction patterns or the zeroth layers of precession photographs (X-ray), dodecagonal QC:  

The pattern above looks similar to the zoom-in in the pattern of the complex division for the interval x=y=[-1..1]. I suspect that the complex division produces those patterns due to a n-fold rotational symmetry. See here for more information too.

3. Credits to Damian OHara. More refraction patterns:

4. In this link there is a very good technical description of the refraction patterns. And in this link there are more examples of n-fold symmetries. In this one there are similar star-like patterns as the ones I found at the roots of quadratic equations.

So far this is all I have found. I will try to look for more information, but at least the similarities are quite interesting.

I would like to finish this post with two of the best videos I found about quasicrystal, tesselations and tiling. The first one is from Sir Roger Penrose, "Forbidden crystal symmetry in mathematics and architecture".

And my favorite one! Professor Marjorie Senechal, "Quasicrystals Gifts to Mathematics":

Please if somebody reading this knows more about the subject let me know, I would like to learn more about it.